ในบทความนี้ เราจะมาทำความรู้จักกับ k-means และวิธีใช้ kmeans() ในภาษา R กัน
- 👉 Introduction to k-Means
- 💻 k-Means ในภาษา R: kmeans()
- 🔢 Dataset
- ⏹️ k-Means
- 😺 GitHub
- 📃 References
- ✅ R Book for Psychologists: หนังสือภาษา R สำหรับนักจิตวิทยา
👉 Introduction to k-Means
.
🤔 k-Means คืออะไร?
k-means เป็น machine learning algorithm ประเภท unsupervised learning และใช้จัดกลุ่ม data (clustering) ที่เราไม่รู้จำนวนกลุ่มล่วงหน้า
ตัวอย่างการใช้ k-means ในโลกจริง:
- Customer segmentation: จัดกลุ่มลูกค้าที่เข้ามาซื้อสินค้า/บริการ
- Anomaly detection: ตรวจจับความผิดปกติในคอมพิวเตอร์ (แบ่งกลุ่มกิจกรรมในคอมพิวเตอร์ เป็น “ปกติ” และ “ไม่ปกติ”)
- Document clustering: จัดกลุ่มเอกสาร โดยอ้างอิงจากเนื้อหา
.
🪜 Steps การทำงานของ k-Means
k-means มีการทำงานอยู่ 5 ขั้นตอน ได้แก่:
- กำหนดจำนวนกลุ่ม หรือ clusters (k)
- สุ่มวาง centroid หรือจุดศูนย์กลางของ cluster ลงในข้อมูล
- จัดกลุ่มข้อมูล โดยข้อมูลจะอยู่กลุ่มเดียวกับ centroid ที่ใกล้ที่สุด
- คำนวณหา centroid ใหม่
- ทำขั้นที่ 3 และ 4 ซ้ำ ตามจำนวนครั้งที่กำหนด หรือจนกว่าข้อมูลจะไม่เปลี่ยนกลุ่ม
ตัวอย่างเช่น เราต้องการจัดกลุ่มข้อมูล 100 ตัวอย่าง:

ขั้นที่ 1. เรากำหนด k เช่น ให้ k = 3
ขั้นที่ 2. สุ่มวาง centroid (ดอกจันสีแดง) ลงในข้อมูล:
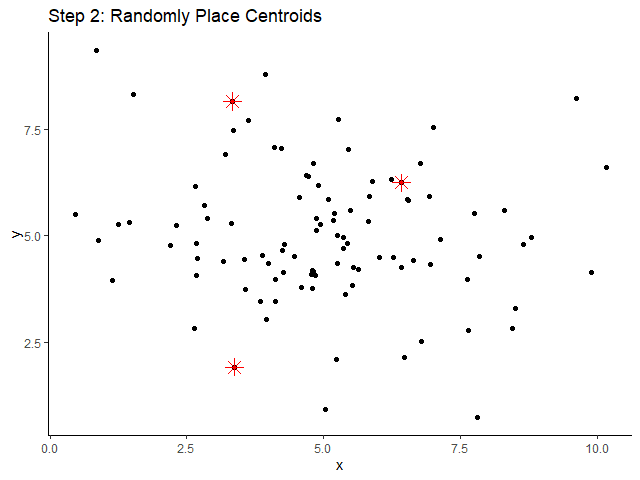
ขั้นที่ 3. จัดข้อมูลให้อยู่กลุ่มเดียวกัน โดยอิงจาก centroid ที่อยู่ใกล้ที่สุด:
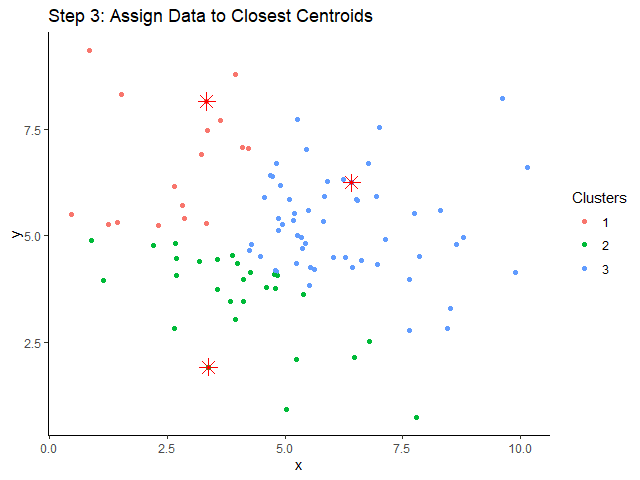
ขั้นที่ 4. คำนวณหา centroids ใหม่:
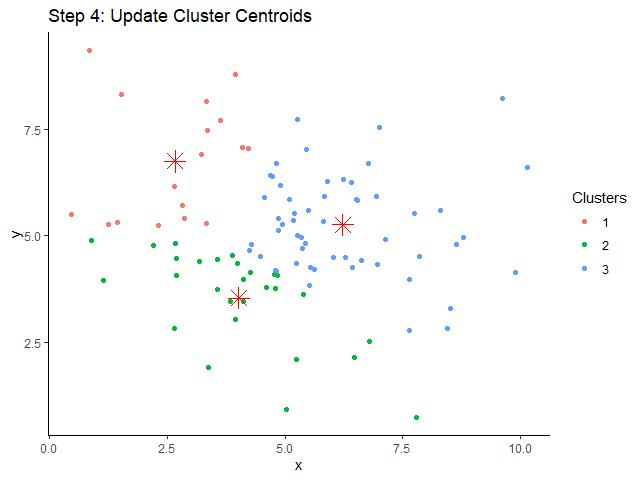
จะสังเกตเห็นว่า centroids ของเราเปลี่ยนไป
ขั้นที่ 5. ทำขั้นที่ 3 และ 4 ซ้ำ ๆ ไปเรื่อย ๆ เช่น ทำไป 10 ครั้ง:

เราก็จะได้การจัดกลุ่มข้อมูลมา
.
🏫 Learn More
เรียนรู้เพิ่มเติมเกี่ยวกับ k-means ได้จากคอร์ส The Nuts and Bolts of Machine Learning จาก Google Career Certificates (เริ่มต้นที่ 1:33:49)
💻 k-Means ในภาษา R: kmeans()
ในภาษา R เราสามารถใช้ k-means ได้ผ่าน kmeans() function ซึ่งต้องการ 3 arguments หลัก ดังนี้:
kmeans(x, centers, nstart)- x = dataset ที่ต้องการจัดกลุ่ม
- centers = จำนวนกลุ่มข้อมูล หรือ k
- nstart = จำนวนครั้งที่ k-means จะสุ่มวาง centroids ลงใน dataset เพื่อหาการจัดกลุ่มที่ดีที่สุด
(Note: ศึกษา arguments เพิ่มเติมของ kmeans() ได้ที่ kmeans: K-Means Clustering)
เราไปดูวิธีใช้งาน kmeans() กัน
🔢 Dataset
.
🪨 rock
ในบทความนี้ เราจะใช้ rock dataset ซึ่งเป็น built-in dataset ในภาษา R เป็นตัวอย่าง
rock มีข้อมูลหิน 48 ตัวอย่าง และมีข้อมูลลักษณะ 4 อย่าง:
| ลำดับ | ลักษณะ | คำอธิบาย |
|---|---|---|
| 1 | area | พื้นที่ผิว |
| 2 | peri | เส้นผ่านศูนย์กลาง |
| 3 | shape | ขนาด (เส้นผ่านศูนย์กลาง หารด้วย พื้นที่ผิว) |
| 4 | perm | ระดับความสามารถที่ให้น้ำซึมผ่านได้ |
เป้าหมายของเรา คือ จัดกลุ่มหิน 48 ตัวอย่างตามลักษณะทั้งสี่
เราสามารถโหลด rock dataset ได้โดยใช้ data() function:
# Load
data(rock)
หลังจากโหลดแล้ว เราสามารถ preview ข้อมูลได้ด้วย head():
# Preview the dataset
head(rock)
ผลลัพธ์:
area peri shape perm
1 4990 2791.90 0.0903296 6.3
2 7002 3892.60 0.1486220 6.3
3 7558 3930.66 0.1833120 6.3
4 7352 3869.32 0.1170630 6.3
5 7943 3948.54 0.1224170 17.1
6 7979 4010.15 0.1670450 17.1
.
📏 Data Normalisation
เนื่องจาก k-means ใช้ระยะห่างระหว่างข้อมูลในการจัดกลุ่ม ข้อมูลที่มีระยะห่างมาก (เช่น ระยะห่าง 500 เมตร กับ 1,000 เมตร) อาจมีผลต่อการจัดกลุ่มมากกว่าข้อมูลที่มีระยะห่างน้อย (เช่น ระยะห่าง 1 ซม. กับ 5 ซม.) และทำให้เกิด bias ในการจัดกลุ่มได้
เพื่อป้องกัน bias เราควร normalise ข้อมูล หรือการปรับให้ข้อมูลอยู่ใน scale เดียวกัน
สำหรับ k-means เรามักจะ normalise ข้อมูล ด้วย z-score standardisation ซึ่งมีสูตรการคำนวณดังนี้:
Z = (X - M(X)) / SD(X)- Z = ข้อมูลที่ scaled แล้ว
- X = ข้อมูลดิบ
- M(X) = mean ของ X
- SD(X) = SD ของ X
ในภาษา R เราสามารถทำ z-score standardisation ได้ด้วย scale():
# Scale
rock_scaled <- scale(rock)
Note: เราใส่ rock ไปใน argument และเก็บผลลัพธ์ไว้ใน data frame ใหม่ ชื่อ rock_scaled
เราสามารถเช็กผลลัพธ์ได้ด้วย:
colMeans()เพื่อเช็ก meanapply()และsd()เพื่อเช็ก SD
# Check the results
## Check mean
round(colMeans(rock_scaled), 2)
# Check SD
apply(rock_scaled, 2, sd)
ผลลัพธ์:
> ### Check mean
> round(colMeans(rock_scaled), 2)
area peri shape perm
0 0 0 0
>
> ### Check SD
> apply(rock_scaled, 2, sd)
area peri shape perm
1 1 1 1
จากผลลัพธ์ เราจะเห็นได้ว่า ทุกลักษณะมี mean เท่ากับ 0 และ SD เท่ากับ 1 แสดงว่า เราทำ z-score standardisation ได้สำเร็จ และพร้อมไปขั้นตอนถัดไป
.
🔎 Finding the Optimal k
ในการจัดกลุ่มด้วย k-means เราต้องเริ่มด้วยการกำหนด k
แต่เราจะรู้ได้ยังไงว่า k ควรมีค่าเท่าไร?
เรามี 3 วิธีในการหาค่า k ที่ดีที่สุด (optimal k):
- Elbow method
- Silhouette analysis
- Gap analysis
ในบทความนี้ เราจะมาใช้วิธีแรกกัน: elbow method
(Note: เรียนรู้เกี่ยวทั้งสามวิธีได้ที่ ML | Determine the optimal value of K in K-Means Clustering)
Elbow method หาค่า k ที่ดีที่สุด โดยสร้างกราฟระหว่างค่า k และ within-cluster sum of squares (WSS) หรือระยะห่างระหว่างข้อมูลในกลุ่ม ค่า k ที่ดีที่สุด คือ ค่า k ที่ WSS เริ่มไม่ลดลง
ในภาษา R เราสามารถเริ่มสร้างกราฟได้ โดยเริ่มจากใช้ for loop หา WSS สำหรับช่วงค่า k ที่เราต้องการ
ในตัวอย่าง rock dataset เราจะใช้ช่วงค่า k ระหว่าง 1 ถึง 15:
# Initialise a vector for within cluster sum of squares (wss)
wss <- numeric(15)
# For-loop through the wss
for (k in 1:15) {
## Try the k
km <- kmeans(rock_scaled,
centers = k,
nstart = 20)
## Get WSS for the k
wss[k] <- km$tot.withinss
}
จากนั้น ใช้ plot() สร้างกราฟความสัมพันธ์ระหว่างค่า k และ WSS:
# Plot the wss
plot(1:15,
wss,
type = "b",
main = "The Number of Clusters vs WSS",
xlab = "Number of Clusters",
ylab = "WSS")
ผลลัพธ์:

จากกราฟ จะเห็นว่า WSS เริ่มชะลอตัว เมื่อค่า k อยู่ที่ 3 และ 4 ซึ่งเป็นจุดที่เป็นข้อศอก (elbow) ของกราฟ:
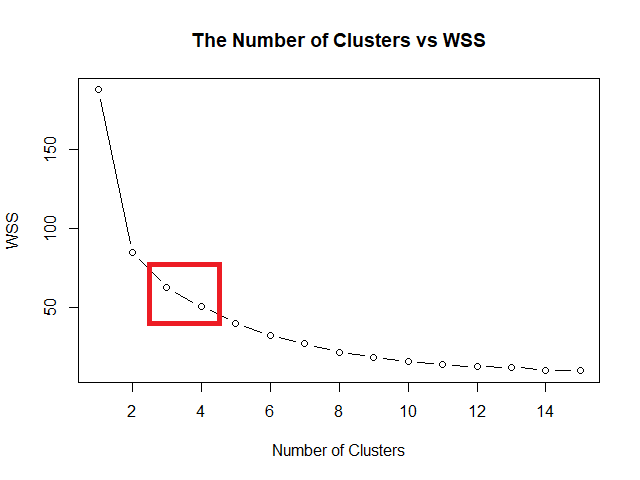
แสดงว่า optimal k มีค่า 3 หรือ 4
สำหรับบทความนี้ เราจะกำหนด optimal k = 4:
# Set optiomal k = 4
opt_k <- 4
⏹️ k-Means
🔥 Train the Model
หลังเตรียมข้อมูลและหา optimal k แล้ว เราก็พร้อมที่จะใช้ kmeans() ในการจัดกลุ่มข้อมูลแล้ว:
# Set see for reproducibility
set.seed(100)
# Train the model
km <- kmeans(rock_scaled,
centers = opt_k,
nstart = 20)
.
🤓 Get the Results
เราสามารถดูผลการจัดกลุ่มได้ 2 วิธี:
วิธีที่ 1. ดูค่าทางสถิติ:
# Print the model
print(km)
ผลลัพธ์:
K-means clustering with 4 clusters of sizes 10, 18, 6, 14
Cluster means:
area peri
1 -0.4406840 -0.9164442
2 0.3496197 0.8022501
3 1.5646450 1.3101981
4 -0.8052989 -0.9383748
shape perm
1 1.5369800 1.1775435
2 -0.7319607 -0.8017914
3 0.2358392 -0.7425075
4 -0.2578245 0.5079897
Clustering vector:
[1] 2 2 2 2 2 2 2 2 2 2 2 2 3
[14] 2 2 2 3 3 3 2 2 3 3 2 1 4
[27] 4 4 4 1 1 1 4 1 4 1 4 1 4
[40] 4 1 4 1 1 4 4 4 4
Within cluster sum of squares by cluster:
[1] 18.917267 8.104718
[3] 1.471788 22.095636
(between_SS / total_SS = 73.1 %)
Available components:
[1] "cluster"
[2] "centers"
[3] "totss"
[4] "withinss"
[5] "tot.withinss"
[6] "betweenss"
[7] "size"
[8] "iter"
[9] "ifault"
จากผลลัพธ์ จะเห็นได้ว่า ข้อมูลถูกแบ่งเป็น 4 กลุ่ม และเราสามารถดูค่า mean และ WSS ของแต่ละกลุ่มได้
.
วิธีที่ 2. สร้างกราฟ:
# Create a plot
plot(rock_scaled[, c("shape", "perm")],
col = km$cluster,
pch = 19,
main = "K-Means Clustering (Rock Dataset)",
xlab = "Shape",
ylab = "Permeability")
# Add cluster centers
points(km$centers[, c("shape", "perm")],
col = 1:5,
pch = 4,
cex = 2,
lwd = 2)
ผลลัพธ์:
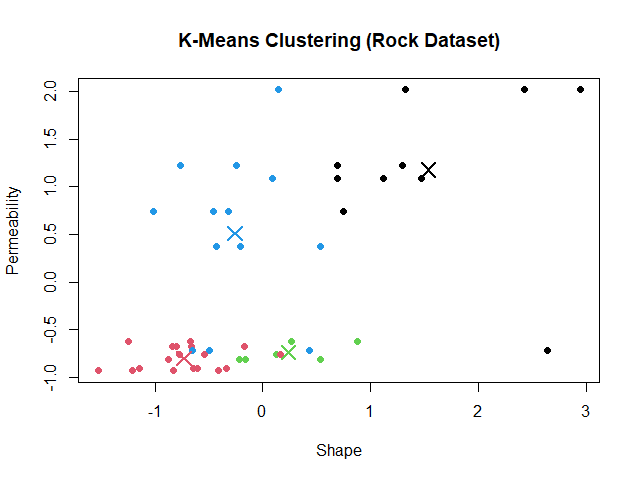
ตอนนี้ เราก็ได้ข้อมูลที่จัดกลุ่มด้วย k-means เรียบร้อยแล้ว 👍
😺 GitHub
ดู code ทั้งหมดในบทความนี้ได้ที่ GitHub
📃 References
- K-Means Clustering in R Tutorial
- What is k-means clustering?
- 8 Machine Learning Algorithms (A quick revision)
- The Nuts & Bolts of Machine Learning
✅ R Book for Psychologists: หนังสือภาษา R สำหรับนักจิตวิทยา
📕 ขอฝากหนังสือเล่มแรกในชีวิตด้วยนะครับ 😆
🙋 ใครที่กำลังเรียนจิตวิทยาหรือทำงานสายจิตวิทยา และเบื่อที่ต้องใช้ software ราคาแพงอย่าง SPSS และ Excel เพื่อทำข้อมูล
💪 ผมขอแนะนำ R Book for Psychologists หนังสือสอนใช้ภาษา R เพื่อการวิเคราะห์ข้อมูลทางจิตวิทยา ที่เขียนมาเพื่อนักจิตวิทยาที่ไม่เคยมีประสบการณ์เขียน code มาก่อน
ในหนังสือ เราจะปูพื้นฐานภาษา R และพาไปดูวิธีวิเคราะห์สถิติที่ใช้บ่อยกัน เช่น:
- Correlation
- t-tests
- ANOVA
- Reliability
- Factor analysis
🚀 เมื่ออ่านและทำตามตัวอย่างใน R Book for Psychologists ทุกคนจะไม่ต้องพึง SPSS และ Excel ในการทำงานอีกต่อไป และสามารถวิเคราะห์ข้อมูลด้วยตัวเองได้ด้วยความมั่นใจ
แล้วทุกคนจะแปลกใจว่า ทำไมภาษา R ง่ายขนาดนี้ 🙂↕️
👉 สนใจดูรายละเอียดหนังสือได้ที่ meb:
